Seperti yang telah dibahas sebelumnya, bahwa titik berat suatu logika adalah pada pembuktian validitas suatu argument logika proposional dengan berbagai teknik yang relevan. Yaitu menggunakan table kebenaran sebagai dasar pembuktian dan dan juga menggunakan hukum-hukum logika.
Logika proposisional sudah cukup untuk menangani pernyataan-pernyataan yang sederhana dan banyak dijumpai dalam peristiwa sehari-hari. Akan tetapi logika proposisional saja ternyata belum mampu menangani argumen-argumen yang berisi pernyataan-pernyataan yang rumit dan sering dijumpai dalam peristiwa sehari-hari.
Misalkan P(x) merupakan sebuah pernyataan yang mengandung variabel x dan D adalah sebuah himpunan. Kita sebut P sebuah fungsi proposisi (dalam D) jika untuk setiap x di D, P(x) adalah proposisi. Kita sebut D daerah asal pembicaraan (domain of discourse) dari P.
Contoh 1:
Berikut ini beberapa contoh fungsi proposisi:
- n² + 2n adalah bilangan ganjil, dengan daerah asal himpunan bilangan bulat.
- x² – x – 6 = 0, dengan daerah asal himpunan bilangan real.
- Seorang pemain bisbol memukul bola melampaui 300 pada tahun 1974, dengan daerah asal himpunan pemain bisbol.Sebuah predikat seringkali menyatakan sebuah hubungan relasional antara: konstanta, variabel dan fungsi.
Simbol-simbol yang digunakan dalam logika predikat:
- Simbol konstanta : a, b, c, d.
- Simbol variabel : x, y, z, w.
- Simbol fungsi : f, g, h.
- Simbol predikat : P, Q, R, S.CONTOH (2)
Beberapa contoh predikat:
- 2x+3 < 5, dengan x bilangan bulat positip dapat ditulis sebagai untuk setiap x (bulat positip), P(x) : f(x) < 5
- x + y ≤ x - y, dengan x dan y bilangan real dapat ditulis sebagai untuk setiap x,y anggota himpunan bilangan (real), Q(x, y) : f(x, y) ≤ g(x, y)
- jika x > 0 maka 4x + 1 > 1, dengan x bilangan bulat dapat ditulis sebagai beberapa x anggota himpunan biangan (bulat), jika R(x) : x > 0, maka S(x) : h(x) > 1
Predikat P(x) menyatakan hubungan relasional antara fungsi f(x) dan konstanta 5. Predikat Q(x; y) menyatakan hubungan relasional antara fungsi f(x; y) dengan fungsi g(x; y). Contoh ketiga memuat penghubung bersyarat "jika ... maka ... " dengan premis predikat R(x) dan konklusi predikat S(x).
2. LOGIKA DAN SET ORDER PERTAMA
Disebut juga kalkulus predikat, merupakan logika yang digunakan untuk merepresentasikan masalah yang tidak dapat direpresentasikan dengan menggunakan proposisi. Logika predikat dapat memberikan representasi fakat-fakta sebagai suatu pernyataan yang mapan (well form). Syarat-syarat symbol dalam logika predikat :
- himpunan huruf, baik huruf kecil maupun huruf besar dalam abjad.
- Himpunan digit (angka) 0,1,2,…9
- Garis bawah “_”
- Symbol-simbol dalam logika predikat dimulai dengan sebuah huruf dan diikuti oleh sembarang rangkaian karakter-karakter yang diijinkan.
- Symbol-simbol logika predikat dapat merepresentasikan variable, konstanta, fungsi atau predikat
Konstanta adalah objek atau sifat dari semesta pembicaraan. Penulisannya diawali dengan huruf kecil, seperti : pohon, tinggi. Konstanta true(benar) dan false(salah) adalah symbol kebenaran (truth symbol).
Variable adalah digunakan untuk merancang kelas objek atau sifat-sifat secara umum dalam semesta pembicaraan. Penulisannya diawali dengan huruf besar, seperti : Bill, Kate.
Fungsi adalah pemetaan (mapping) dari satu atau lebih elemen dalam suatu himpunan yang disebut domainfungsi ke dalam sebuah elemen unik pada himpunan lain yang disebut rangefungsi. Penulisannya dimulai dengan huruf kecil. Suatu ekspresi fungsi merupakan symbol fungsi yang diikuti argument.
Argument adalah elemen-elemen dari fungsi, ditulis diapit tanda kurung dan dipisahkan dengan tanda koma.
Predikat adalah menamai hubungan antara nol atau lebih objek dalam semesta pembicaraan. Penulisannya dimulai dengan huruf kecil, seperti : equals, sama dengan, likes, near.
Contoh kalimat dasar :
teman(george,allen)
teman(ayah_dari(david),ayah_dari(andrew))
dimana :
argument : ayah_dari(david) adalah george
argument : ayah_dari(andrew) adalah allen
predikat : teman
3. QUANTIFIER UNIVERSAL
Dalam logika predikat , kuantifikasi universal merupakan jenis quantifier , sebuah konstanta logis yang ditafsirkan sebagai "diberi" atau "untuk semua". Ini mengungkapkan bahwa fungsi proposisi dapat dipenuhi oleh setiap anggota dari domain wacana. Dalam istilah lain, itu adalah predikasi dari properti atau hubungan dengan setiap anggota domain. Ini menegaskan bahwa predikat dalam lingkup dari quantifier universal benar dari setiap nilai dari variabel predikat .
Hal ini biasanya dilambangkan dengan berbalik A (∀) operator logika simbol , yang bila digunakan bersama-sama dengan variabel predikat, disebut quantifier universal ("∀x", "∀ (x)", atau kadang-kadang dengan "(x) "saja). Kuantifikasi Universal berbeda darikuantifikasi eksistensial ("ada ada"), yang menegaskan bahwa properti atau relasi hanya berlaku untuk setidaknya satu anggota dari domain.
- Contoh 1 :
(∀x) (x + x = 2x)
“untuk setiap x (dimana x adalah suatu bilangan), kalimat x + x = 2x adalah benar.” - Contoh 2 :
(∀x) (p) (Jika x adalah seekor kucing -> x adalah binatang).
Kebalikan kalimat “bukan kucing adalah binantang” ditulis :
(∀x) (p) (Jika x adalah seekor kucing -> ~x adalah binatang)
dan dibaca :
- “setiap kucing adalah bukan binantang”
-“semua kucing adalah bukan binantang” - Contoh 3:
(∀x) (Jika x adalah segitiga -> x adalah polygon)
Dibaca : “untuk semua x, jika x adalah segitiga, maka x adalah polygon”.
Dapat pula ditulis : (∀x) (segitiga(x) -> polygon(x))
(∀x) (T(x) P(x)) - Contoh 4 :
(∀x) (H(x) M(x))
Dibaca : “untuk semua x, jika x adalah manusia (human), maka x melahirkan (mortal)”.
Ditulis dalam aturan : IF x adalah manusia THEN x melahirkan
Digambar dalam jaringan semantic :
4. QUANTIFIER EXISTENSIAL
Dalam logika predikat , suatu kuantifikasi eksistensial adalah jenis quantifier , sebuah konstanta logis yang ditafsirkan sebagai "ada ada," "ada setidaknya satu," atau "untuk beberapa." Ini mengungkapkan bahwa fungsi proposisi dapat dipenuhi oleh setidaknya satuanggota dari domain wacana . Dalam istilah lain, itu adalah predikasi dari properti atau hubungan dengan setidaknya satu anggota dari domain. Ini menegaskan bahwa predikat dalam lingkup dari quantifier eksistensial adalah benar dari setidaknya satu nilai dari variabel predikat.
Hal ini biasanya dilambangkan dengan E berubah (∃) operator logika simbol , yang bila digunakan bersama-sama dengan variabel predikat, disebut quantifier eksistensial ("∃x" atau "∃ (x)"). Kuantifikasi eksistensial berbeda dari kuantifikasi universal ("untuk semua"), yang menegaskan bahwa properti atau hubungan berlaku untuk semua anggota domain.
- Contoh 1 :
(∃x) (x . x = 1)
Dibaca : “terdapat x yang bila dikalikan dengan dirinya sendiri hasilnya sama dengan 1.” - Contoh 2 :
(∃x) (gajah(x) ∧ nama(Clyde))
Dibaca : “beberapa gajah bernama Clyde”. - Contoh 3 :
(∀x) (gajah(x) berkaki empat(x))
Dibaca : “semua gajah berkaki empat”.
(∃x) (gajah(x) ∧ berkaki tiga(x))
Dibaca : “ada gajah yang berkaki tiga”
Existensial quantifier dapat diekspresikan sebagai disjungsi dari
urutan ai. P(a1) ∨ P(a2) ∨ P(a3) …∨ P(aN)
Quantifier dan Set / Jaringan
Set Expression
|
Logical Equivalent
|
A = B
|
∀x (x ∈A ↔x ∈B)
|
A ⊆B
|
∀x (x ∈A ->x ∈B)
|
A ∩B
|
∀x (x ∈A ∧x ∈B)
|
A ∪B
|
∀x (x ∈A ∨x ∈B)
|
μ(universe)
|
T (True)
|
φ(empty set)
|
F (False)
|
- Relasi A proper subset dari B ditulis A ⊂B, dibaca “semua elemen A ada pada B”, dan “paling sedikit satu elemen B bukan bagian dari A”.
- Hukum de Morgan berlaku untuk analogi himpunan dan bentuk logika :
Himpunan
|
Logika
|
(A∩B)≡A’∪B’
|
~(p∧q) ≡p∨~q
|
(A∪B)≡A’∩B’
|
~(p∨q) ≡p ∧~q
|
Diketahui :
E = elephant
R = reptile
G = gray
F = four legged
D = dogs
M = mammals
Set expression
|
Berarti
|
E ⊂M
|
“elephant termasuk mammals”, tetapi tidak semua mammals adalah elephant
|
(E ∩G ∩F) ⊂M
|
“elephant yang berwarna gray dan memiliki four legged termasuk mammals”
|
E ∩R = φ
|
“tidak ada elephant yang termasuk reptile”
|
E ∩G ≠φ
|
“beberapa elephant berwarna gray”
|
E ∩G = φ
|
“tidak ada elephant yang berwarna gray”
|
E ∩G’≠φ
|
“beberapa elephants tidak berwarana gray”
|
E ⊂(G ∩F)
|
“semua elephants berwarna gray dan memiliki four legged”
|
(E ∪D) ⊂M
|
“semua elephants dan dogs termasuk mammals”
|
(E ∩F ∩G) ≠φ
|
“beberapa elephants memiliki four legged dan berwarna gray”
|
5. RESOLUSI LOGIKA PREDIKAT
Resolusi pada logika predikat pada dasarnya sama dengan resolusi pada logika proposisi, hanya saja ditambah dengan unufikasi. Pada logika predikat, prosedur untuk membuktikan pernyataan P dengan beberapa pernyataan F yang telah diketahui, dengan menggunakan resolusi, dapat dilakukan melalui algoritma sebagai berikut:
- Konversikan semua proposisi F ke bentuk klausa.
- Negasikan P, dan konversikan hasil negasi tersebut ke bentuk klausa. Tambahkan ke himpunan klausa yang telah ada pada langkah 1.
- Kerjakan hingga terjadi kontradiksi atau proses tidak mengalami kemajuan:
a. Seleksi 2 klausa sebagai klausa parent.
b. Bandingkan (resolve) secara bersama-sama. Klausa hasil resolve tersebut dinamakan resolvent. Jika ada pasangan literal T1 dan T2 sedemikian hingga keduanya dapat dilakukan unifikasi, maka salah satu T1 atau T2 tidak muncul lagi dalam resolvent. T1 dan T2 disebut sebagai complementary literal. Jika ada lebih dari 1 complementary literal, maka hanya sepasang yang dapat meninggalkan resolvent.
c. Jika resolvent berupa klausa kosong, maka ditemukan kontradiksi. Jika tidak, tambahkan ke himpunan klausa yang telah ada.
Contoh :
Misalkan terdapat pernyataan-pernyataan sebagai berikut :
- Andi adalah seorang mahasiswa.
- Andi masuk Jurusan Elektro.
- Setiap mahasiswa elektro pasti mahasiswa teknik.
- Kalkulus adalah matakuliah yang sulit.
- Setiap mahasiswa teknik pasti akan suka kalkulus atau akan membencinya.
- Setiap mahasiswa pasti akan suka terhadap suatu matakuliah.
- Mahasiswa yang tidak pernah hadir pada kuliah matakuliah sulit, maka mereka pasti tidak suka terhadap matakuliah tersebut.
- Andi tidak pernah hadir kuliah matakuliah kalkulus.
Kedelapan pernyataan di atas dapat dibawa ke bentuk logika predikat, dengan menggunakan operator-operator logika predikat, sebagai berikut : - mahasiswa(Andi).
- Elektro(Andi).
- ∀x:Elektro(x)→Teknik(x).
- sulit(Kalkulus).
- ∀x:Teknik(x) → suka(x,Kalkulus) ∨ benci(x,Kalkulus).
- ∀x:∃y:suka(x,y).
- ∀x:∀y:mahasiswa(x)∧sulit(y) ∧ ¬hadir(x,y)→ ¬suka(x,y).
- ¬hadir(Andi,Kalkulus).
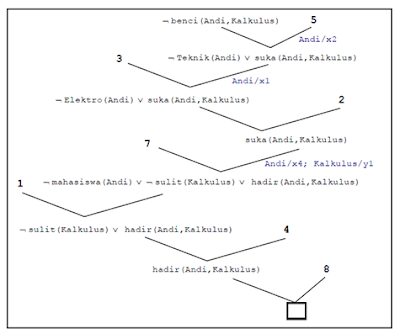
Kita dapat membawa pernyataan-pernyataan yang ada menjadi bentuk klausa (CNF) sebagai berikut:
- mahasiswa(Andi).
- Elektro(Andi).
- ¬Elektro(x1) ∨ Teknik(x1).
- sulit(Kalkulus).
- ¬Teknik(x2) ∨ suka(x2,Kalkulus) ∨ benci(x2,Kalkulus).
- suka(x3,fl(x3)).
- ¬mahasiswa(x4) ∨ ¬sulit(y1) ∨ hadir(x4,y1) ∨ ¬suka(x4,y1).
- ¬hadir(Andi,Kalkulus).
Sumber Referensi:
Tidak ada komentar:
Posting Komentar