INFERENSI DALAM LOGIKA ORDER PERTAMA

1. MENGUBAH INFERENSI ORDER PERTAMA MENJADI INFERENSI PROPOSISI

(First Order Predicate Logic)
Representasi 4 kategori silogisme menggunakan logika predikat

Kaidah Universal Instatiation merupakan state dasar, dimana suatu individual dapat digantikan (disubsitusi) ke dalam sifat universal.

Contoh :

Misal, φ merupakan fungsi proposisi :

(∀ x) φ(x)

∴ φ(a)

merupakan bentuk yang valid, dimana a menunjukkan spesifik individual, sedangkan x adalah suatu variabel yang berada dalam jangkauan semua individu (universal)

Contoh lain : (∀ x) H(x)

∴ H(Socrates)

• Berikut ini adalah contoh pembuktian formal silogisme

All men are mortal

Socrates is a man

Therefore, Socrates is mortal

Misal : H = man, M = mortal, s = Socrates

1. (∀ x) (H (x) -> M(x))

2. H(s) / ∴ M(s)

3. H(s) -> M(s) 1 Universal Instatiation

4. M(s) 2,3 Modus Ponens

2. UNIFIKASI

Unifikasi adalah usaha untuk mencoba membuat dua ekspresi menjadi identik (mempersatukan keduanya) dengan mencari substitusi-substitusi tertentu untuk mengikuti peubah-peubah dalam ekspresi mereka tersebut. Unifikasi merupakan suatu prosedur sistematik untuk memperoleh peubah-peubah instan dalam wffs. Ketika nilai kebenaran predikat adalah sebuah fungsi dari nilai-nilai yang diasumsikan dengan argumen mereka, keinstanan terkontrol dari nilai-nilai selanjutnya yang menyediakan cara memvalidasi nilai-nilai kebenaran pernyataan yang berisi predikat. Unifikasi merupakan dasar atas kebanyakan strategi inferensi dalam Kecerdasan Buatan. Sedangkan dasar dari unifikasi adalah substitusi.

Suatu substitusi (substitution) adalah suatu himpunan penetapan istilah-istilah kepada peubah, tanpa ada peubah yang ditetapkan lebih dari satu istilah. Sebagai pengetahuan jantung dari eksekusi Prolog, adalah mekanisme unifikasi.

Aturan-aturan unifikasi :

1. Dua atom (konstanta atau peubah) adalah identik.
2. Dua daftar identik, atau ekspresi dikonversi ke dalam satu buah daftar.
3. Sebuah konstanta dan satu peubah terikat dipersatukan, sehingga peubah menjadi terikat kepada konstanta.
4. Sebuah peubah tak terikat dipersatukan dengan sebuah peubah terikat.
5. Sebuah peubah terikat dipersatukan dengan sebuah konstanta jika pengikatan pada peubah terikat dengan konstanta tidak ada konflik.
6. Dua peubah tidak terikat disatukan. Jika peubah yang satu lainnya menjadi terikat dalam upa-urutan langkah unifikasi, yang lainnya juga menjadi terikat ke atom yang sama (peubah atau konstanta).
7. Dua peubah terikat disatukan jika keduanya terikat (mungkin melalui pengikatan tengah) ke atom yang sama (peubah atau konstanta).

3. GENERALIZED MODUS PONENS (GMP)

Dalam logika proposisional , modus ponendo ponens ( Latin untuk "cara yang menegaskan dengan menegaskan"; umumnya disingkat MP atau modus ponens) atau implikasi penghapusan adalah aturan inferensi. Hal ini dapat diringkas sebagai "Pmenyiratkan Q dan P menegaskan untuk menjadi kenyataan, jadi karena Q harus benar." Sejarah modus ponens kembali ke jaman dahulu.

Modus ponens berkaitan erat dengan bentuk lain valid argumen, modus tollens . Keduanya memiliki bentuk rupanya mirip tapi tidak valid seperti menegaskan konsekuen , menyangkal anteseden , dan bukti adanya . Dilema konstruktif adalah disjungtif versi modus ponens. Silogisme hipotetis berkaitan erat dengan modus ponens dan kadang-kadang dianggap sebagai "modus ponens ganda."

Notasi  Formal

The modus ponens aturan dapat ditulis dalam berturut-turut notasi: 

mana ⊢ adalah metalogical simbol yang berarti bahwa Q adalah konsekuensi sintaksis dari P → Q dan P dalam beberapa sistem logis ;

atau sebagai pernyataan dari kebenaran-fungsional tautologi atau teorema logika proposisional:

di mana P, dan Q adalah proposisi yang dinyatakan dalam beberapa sistem resmi.

Penjelasan

Bentuk argumen memiliki dua tempat (hipotesis). Premis pertama adalah "jika-maka" atau bersyarat klaim, yaitu bahwa P menyiratkan Q. Premis kedua adalah bahwa P, yang klaim bersyarat, benar. Dari dua premis tersebut dapat secara logis menyimpulkan bahwa Q, yang konsekuen dari klaim bersyarat, harus benar juga. Pada kecerdasan buatan , modus ponens sering disebut forward chaining .

Contoh argumen yang sesuai dengan modus ponens bentuk:

Jika hari ini adalah hari Selasa, maka John akan pergi bekerja.

Hari ini adalah hari Selasa.

Oleh karena itu, John akan pergi bekerja.

Argumen ini berlaku, tapi ini tidak memiliki bantalan pada apakah salah satu pernyataan dalam argumen yang benar ; untuk modus ponens menjadi argumen suara, tempat harus benar untuk setiap kasus sejati kesimpulan. Sebuah argumen dapat berlaku tapi tetap sehat jika satu atau lebih tempat yang palsu; jika argumen valid dan semua tempat yang benar, maka argumen adalah suara. Sebagai contoh, John mungkin akan bekerja pada hari Rabu. Dalam hal ini, alasan untuk John akan bekerja (karena Rabu) adalah tidak sehat. Argumen tersebut tidak hanya terdengar pada hari Selasa (ketika John pergi bekerja), tapi berlaku pada setiap hari dalam seminggu. Sebuah proposisi argumen menggunakan modus ponens dikatakan deduktif .

Dalam single-kesimpulan sequent bate , modus ponens adalah aturan Cut. The cut-eliminasi teorema untuk kalkulus mengatakan bahwa setiap bukti yang melibatkan Cut dapat diubah (umumnya, dengan metode konstruktif) ke bukti tanpa Cut, dan karenanya bahwa Cut adalah diterima .

The Curry-Howard korespondensi antara bukti dan program berhubungan modus ponens ke fungsi aplikasi : jika f adalah fungsi dari jenis P → Q dan x adalah tipe P, maka fxadalah tipe Q.

Pembelajaran melalui Tabel Kebenaran

Validitas modus ponens di klasik dua-nilai logika dapat dibuktikan dengan jelas dengan menggunakan sebuah tabel kebenaran.

Dalam contoh modus ponens kita asumsikan sebagai denga bahwa p → q benar dan p benar. Hanya satu baris dari tabel kebenaran-pertama-memenuhi dua kondisi (p dan p → q). Pada baris ini, q juga benar. Oleh karena itu, setiap kali p → q benar dan p benar, q juga harus benar.

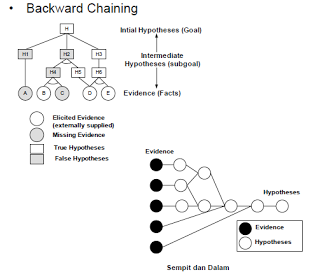
4. RANGKAIAN FORWARD DAN BACKWARD

• Chain (rantai) : perkalian inferensi yang menghubungkan suatu permasalahan denga solusinya.
• Forward chaining :
  – Suatu rantai yang dicari atau dilewati/dilintasi dari suatu permasalahn untuk memperoleh solusi.
  – Penalaran dari fakta menuju konklusi yang terdapat dari fakta.
• Backward chaining :
  – Suatu rantai yang dilintasi dari suatu hipotesa tersebut.
  – Tujuan yang dapat dipenuhi dengan pemenuhan sub tujuannya.
• Contoh rantai inferensi :
  gajah(x) -> mamalia (x)
  mamalia(x) -> binatang(x)

Karakteristik Forward dan Backward Chaining

Forward Chaining

Backward Chaining

Sumber Referensi:

https://kusikhsanto.wordpress.com/2010/04/14/inferensi-dan-implikasi-pada-penalaran/

https://en.wikipedia.org/wiki/Modus_ponens

https://www.academia.edu/9763118/Metode_Inferensi_1_54_Pengantar_Kecerdasan_Buatan_AK045218